Triangulation of Simple Polygons
Ben Discoe, notes from 2001.02.11, updated through 2009.01

I needed some code for tessellating polygons, which could be integrated into the VTP libraries, with the following desirable traits:

• portable
• no dependencies on large external libraries
• free (no restrictive license)
• in C/C++
• easy to use
• preferably, handles 'holes' in the polygon

Here are each of the options i found.

1. OpenGL
   • contains functionality (in the glu library) which is capable of tessellation
   • problem: requires a complicated system of registering 6 callback functions
   • problem: not easy to use, no example code in Red Book
   • problem: has large external dependency (OpenGL, with a valid context)
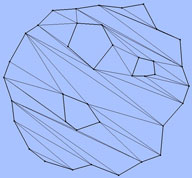   • Extracting the gluTessellate functionality from the SGI OpenGL® Sample Implementation
     • one developer has done this, and says "It was very easy", which seems rather surprising!
   • Valéry Moya wrote in July 2009:
     • "I wrote my own glu tesselator. Grabbing the tessellation from the callbacks isn't all that hard and doesn't require too much code to get working.  (In fact, I got it working with just 2 of the callbacks registered:  GLU_TESS_BEGIN and GLU_TESS_VERTEX.)   In my trial, I was able to get tessellations from lists verts that make up the contour of the polygon I wanted to tessellate (with no overlapping edged, but allowing holes defined as counterclockwise list of verts).  The "hard" part is that you need to handle getting the triangulated verts as triangles, triangle fans and triangle strip order but this not as bad as it sounds to keep track of. "
     • Val's code: glu_tesselation.c
2. Fast Polygon Triangulation based on Seidel's Algorithm (1995)
   • has C code available
   • problem: small Unix dependency (<sys/time.h>), calls nonstandard stdlib function "log2"
   • problem: in the function add_segment(), a variable is used without being initialized - i.e. it's questionable code
   • problem? the README written in 1995 says "for non-commercial use only"
     • the author Atul Narkhede, who went from CMU to SGI, refers to the code on a more current website as specifically "Public Domain", so the latest status is apparently non-restrictive
   • 2008, received an email from another guy trying the code, and he found the code was too buggy
3. Efficient Polygon Triangulation, by John W. Ratcliff on flipcode
   • C++ code, very small and easy to use!
   • Uses STL, but this dependency was easy to remove
   • Tested it on my own data, it worked very well.  Add it to vtdata.
   • Only one problem: doesn't handle holes (and doesn't claim to)
4. GPC
   • does clipping and boolean operations in addition to triangulation
   • problem: reportedly "uses a simple trapezoidal decomposition that introduces lots of t-junctions"
   • problem: prohibitive license restricts usage
5. "Triangle" by Jonathan Shewchuk
   • Can produce Delaunay triangulations, which apparently have desirable traits for some purposes, but are a bit overkill for the general case.  For our simpler case it can produce "Constrained Delaunay", which means no extraneous triangles.
   • Supports holes!
   • Source is free and portable, only one source file (triangle.c) which makes it easy to integrate with.
   • One small drawback: You can't just tell it which segments are the edges of your hole.  Instead, you must supply some point that lies within the hole.  Triangle triangulate the hole, then does some kind of "flood fill" to empty it.  It's inefficient, but what's worse is it requires the caller to compute a point-in-polygon for the hole.  This is a non-trivial algorithm for an arbitrary complex polygon.
   • In 2008.01, i adapted the Triangle code with a wrapper to call it from vtlib.  It works quite well, for a very large number of polygons.  However, there are some (rare) cases of degenerate geometry where it will crash.  In particular:
     1. It does not like duplicate vertices or duplicate edges.  'Duplicate' in this case is relative to numeric precision: For a building 10-100 meters in size, two vertices within 8cm of each other, defining a very short edge, can cause Triangle to crash.
     2. It does not like it when a hole (inner ring) in the polygon has a vertex in the same location as one in the outer ring (crash).
6. TerraGear
   • a Free library which contains a cleaned-up version of the Narkhede implementation of the Seidel algorithm (above)?  No.  Perhaps it did back in 2001, but as of 2007, it contains code to call "Triangle".  It is actually useful as good example code of how to call Triangle.
7. Panda3d
   • A huge, free software stack used by Disney's VR group, which includes triangulation adapted from "Narkhede A. and Manocha D., Fast polygon triangulation algorithm based on Seidel's Algorithm"
   •  The triangulation is buried deep in the C++ part of its code, underneath a massive mess of python, tcl, cross-platform abstraction, and custom build tools used to build custom build tools!
   • On 2008.01.30, i lifted the 'Triangulate' module out of Panda, made it standalone, and ran the provided test (test_tri.cxx).  It crashed, with a negative array index.
   • I also spent 3 hours trying to build Panda itself (with most dependencies including Python disabled.)  No luck, it is just too complex.
   • There were some implications that the Panda version of Narkhede-Manocha might be cleaned up or fixed.  However, since it crashes (for me) on a simple test outside of Panda, this is not encouraging.
   • From: Sébastien Berthet [mailto:sbrt@yahoo.fr]
Sent: Friday, February 01, 2008 12:56 AM
I assume that you used the last version on CVS (commited 3 weeks ago), right ?  http://panda3d.cvs.sourceforge.net/panda3d/panda/src/mathutil/triangulator.cxx?revision=1.5&view=markup
The thread on the forum mentions a few fixes...
8. Poly2Tri (Liang / Kittelman, 2005)
   • "Subdivision using monotone polygons and a sweep line algorithm, O(n log n) time and O(n) storage"
   • Supports holes, makes a lot of very skinny triangles.
   • It compares the speed of Poly2Tri vs. some other triangulation implementations, and it claims to be faster, although the triangles produced are very skinny slivers.
   • Another open source implementation is available at PolygonTriangulator.cxx (google it), by Thomas Kittelmann, which says it is adapted from the implementation by Wu Liang (2005), which appears to be part of a project called "Atlas LXR"
9. poly2tri (Mason Green?, 2009-)
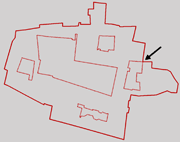
   • Says it is "Based on the paper Sweep-line algorithm for constrained Delaunay triangulation by V. Domiter and and B. Zalik"
   • Handles holes.
   • BSD license.  Lives on google-code.
   • I evaluated it on 2011-07-19.  It managed to tessellate some input which Shewchuk's Triangle couldn't not.  However, it still crashed on some input, like the polygon to the right.  Notice how, once again, one of the polygon's holes (inner rings) exactly touches the outer ring.  The algorithm seems to regard this as degenerate (and does not even detect it to avoid crashing) but it is unfortunately a commonly encountered shape.
10. JTS
    • The Java Topology Suite (JTS) as of 2011 will apparently do reasonable quality triangulation and support holes, see Polygon Triangulation via Ear-Clipping with Delaunay Refinement.  JTS is a very large package (as is its C++ sibling, GEOS) but if you are already using it, then this might be an option.

Others

• Triangulating a Simple Polygon in Linear Time (Chazelle 1991)
• M. Held (2001): "FIST: Fast Industrial-Strength Triangulation of Polygons". FIST is not open source nor allows unrestricted use.